In geometry, parallel lines are two or more lines that remain equidistant from each other at all points and never intersect, regardless of how far they are extended. Parallelism is a fundamental concept in both Euclidean geometry and everyday applications, where it serves to establish stability, balance, and symmetry.
Understanding parallel lines involves recognizing certain key properties and relationships, often involving angles and specific measurements This article delves into the methods and principles used to determine whether lines are parallel, providing justification through mathematical reasoning.
What Are Parallel Lines?
Parallel lines are lines in the same plane that do not meet, no matter how far they are extended. A well-known visual example of parallel lines can be seen in railway tracks, which remain an equal distance apart and do not converge. Symbolically, two parallel lines are usually denoted with a double-bar notation, such as AB∥CDAB \parallel CDAB∥CD.
Properties of Parallel Lines
To understand what makes lines parallel, let’s look at some basic properties:
- Equidistant: Parallel lines remain the same distance apart at all points along their lengths.
- Never Intersect: By definition, parallel lines do not cross or meet, regardless of how long they are extended.
- Same Plane: Parallel lines exist within the same plane. Lines that do not intersect and are not in the same plane are called skew lines, which are not considered parallel.
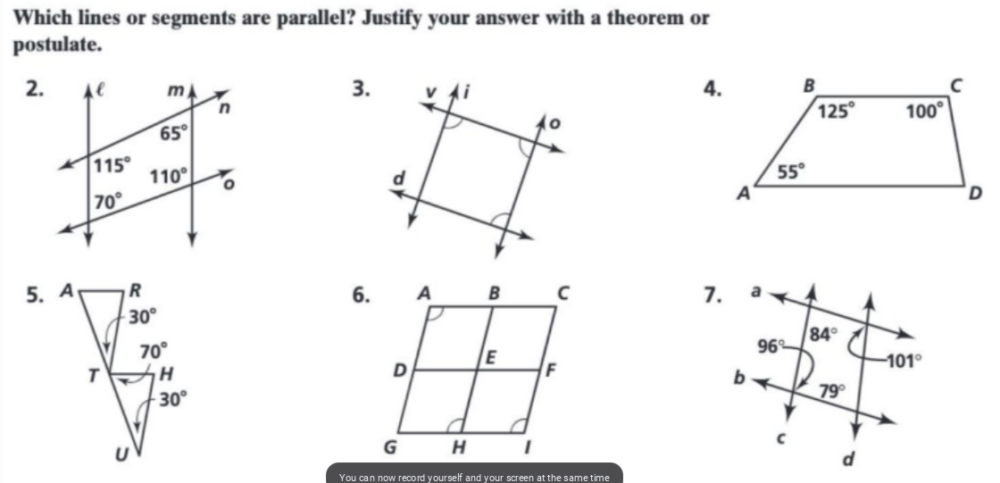
Key Criteria for Determining Parallel Lines
In geometry, several criteria are used to identify parallel lines based on angle relationships when a transversal (a line that intersects two or more lines) crosses the lines. Let’s explore these criteria in more detail:
- Corresponding Angles: When a transversal intersects two lines, corresponding angles are formed on the same side of the transversal and in the same relative positions. If the corresponding angles are congruent (equal in measure), then the two lines are parallel. For example, if angle ∠1=∠2\angle 1 = \angle 2∠1=∠2, where ∠1\angle 1∠1 and ∠2\angle 2∠2 are corresponding angles, then the lines are parallel.
- Alternate Interior Angles: Alternate interior angles are formed when a transversal intersects two lines and they lie on opposite sides of the transversal but inside the two lines. If these angles are congruent, the lines are parallel. For instance, if ∠3=∠4\angle 3 = \angle 4∠3=∠4 where ∠3\angle 3∠3 and ∠4\angle 4∠4 are alternate interior angles, then the lines are parallel.
- Alternate Exterior Angles: Similarly, alternate exterior angles are angles that lie on opposite sides of the transversal and outside the two intersected lines. If alternate exterior angles are congruent, then the lines are parallel.
- Consecutive Interior Angles (or Same-Side Interior Angles): Consecutive interior angles are located on the same side of the transversal and between the two lines. If these angles are supplementary (add up to 180 degrees), then the lines are parallel. For instance, if ∠5+∠6=180∘\angle 5 + \angle 6 = 180^\circ∠5+∠6=180∘, where ∠5\angle 5∠5 and ∠6\angle 6∠6 are consecutive interior angles, the lines are parallel.
Using Slopes to Determine Parallelism
In a coordinate plane, the slopes of lines provide a straightforward way to check for parallelism. The slope of a line represents its steepness or incline and is calculated as the ratio of the vertical change to the horizontal change between two points on the line. Lines with identical slopes are parallel because they incline at the same rate. Here’s how to apply the slope concept to determine parallelism:
- Calculate the Slope: For two points (x1,y1)(x_1, y_1)(x1,y1) and (x2,y2)(x_2, y_2)(x2,y2) on a line, the slope mmm is given by the formula:m=y2−y1x2−x1m = \frac{y_2 – y_1}{x_2 – x_1}m=x2−x1y2−y1
- Compare Slopes: If two lines have the same slope, they are parallel. For example, if the slope of line L1L_1L1 is equal to the slope of line L2L_2L2, then L1∥L2L_1 \parallel L_2L1∥L2.
- Vertical and Horizontal Lines: Vertical lines (having an undefined slope) and horizontal lines (having a slope of zero) are also parallel if they run along the same orientation. For instance, two vertical lines are always parallel because they do not intersect as they extend indefinitely in a vertical direction.
Real-World Examples of Parallel Lines
Understanding parallelism has practical applications in various fields:
- Architecture: Buildings often have parallel beams or floors to provide structural balance.
- Transportation: Railway tracks and road lanes are parallel to ensure smooth and safe travel.
- Graphic Design: Parallel lines are used in designs to create balance and symmetry.
Justifying Parallelism: Example Problems
Let’s apply the concepts discussed to solve some example problems.
Example 1: Identifying Parallel Lines with Angles
Suppose two lines, L1L_1L1 and L2L_2L2, are cut by a transversal, creating pairs of corresponding, alternate interior, and consecutive interior angles. We observe the following:
- ∠A\angle A∠A and ∠B\angle B∠B are corresponding angles, and ∠A=120∘\angle A = 120^\circ∠A=120∘ while ∠B=120∘\angle B = 120^\circ∠B=120∘.
- Since corresponding angles are congruent, L1∥L2L_1 \parallel L_2L1∥L2 by the corresponding angles postulate.
Example 2: Using Slope to Identify Parallel Lines
Let’s consider two lines with the following points:
- Line L1L_1L1: Points (2, 3) and (4, 7)
- Line L2L_2L2: Points (1, -1) and (3, 3)
First, we calculate the slope of L1L_1L1:m1=7−34−2=42=2m_1 = \frac{7 – 3}{4 – 2} = \frac{4}{2} = 2m1=4−27−3=24=2
Now, the slope of L2L_2L2:m2=3−(−1)3−1=42=2m_2 = \frac{3 – (-1)}{3 – 1} = \frac{4}{2} = 2m2=3−13−(−1)=24=2
Since m1=m2=2m_1 = m_2 = 2m1=m2=2, the lines L1L_1L1 and L2L_2L2 are parallel by the slope criterion.

Common Misconceptions About Parallel Lines
- Same Length Requirement: People often mistakenly think that parallel lines must be of the same length. However, lines can be of different lengths and still be parallel.
- Intersecting Lines in 3D Space: In three-dimensional geometry, lines that do not intersect are not necessarily parallel; they could be skew lines, existing in different planes.
Conclusion
Determining whether lines are parallel requires recognizing specific angle relationships or calculating slopes, depending on the context. Through principles like corresponding and alternate angles,
as well as the consistency of slopes, we can verify parallelism in both theoretical and practical settings. Understanding parallelism enriches our ability to work with geometric structures and design stable, symmetrical forms in both mathematics and real-world applications.